What are Markov Chains, and how to use them to generate sentences?

Henlo ma friands!

Some times ago, I developped a bot that allows me to generate sentences from gathered tweets. The code of the bot is available here, and here's an example of an input, and an output :

• Input : py main.py -a Coul33t -n -p 20 -m 3 -r (You can read the bot's Github page to understand what does the different parameters do)
• Output : Je donne 1h de la musique en ligne dans les neurones de l'homme et la détresse des gens. I now have a l w a y s (I give 1 hour of online music in the man's neuron and people's distress. I now have a l w a y s )

As you can see, it does not make a lot of sense, but the sentence seems to " have something " coherent in it. The output is generated from my tweets, by " mixing " them together, in a kinda-coherent way.

It uses Markov Chains (I developped the Markov Chains library used in the bot by myself, so it's probably messy and not optimal at all) to achieve this. Now, there are some way better ways to do it nowadays (mainly with the famous Neural Networks), but Markov Chains have the advantage of being easily understandable, and kinda easy to implement.

What is a Markov Chain?

I could put the Wikipedia definition here, but I think that knowing that

a Markov chain is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event

wouldn't be very helpful. Well, actually, some parts of it are interesting, mainly this one:

the probability of each event depends only on the state attained in the previous event

From this part of the sentence, we can understand that a Markov chain has events and probabilities that are conjointly used: you have a probability to go from an event to another.

Let's take an example of such a system. I will describe my typical evening/night. For the sake of simplicity, I will only use a small subset of what I usually do. When I come home, I wash my hands, then I usually sit at my desk, playing vidayagames. But sometimes, I play the guitar or the piano or the bass, depending on my mood. Then, if it isn't too late, I go back playing VIDAYAGUMZ, until I decide it's time to go to sleep. Let put some labels on those activities:

• H : coming home
• W : washing hands
• V : playing videogames
• I : playing an instrument (either the guitar, the piano or the bass)
• S : going to sleep

Ok, we got our events. Now, when I come home, I usually play videogames before playing any instruments. So there a higher probability that I'll play vuduogumz than an instrument, roughly 75%/25%. When I'm playing videogames, I usually play for a few hours before doing something else. When I play an instrument, I usually play for one hour (sometimes different instruments in this hour). If we decide that we want to represent the chances to switch from an activity to another every hour, we can build an array of probabilities for each event pair of events we have. The first column represent the current event (X), the first row represent the next event (Y), and the value at the crossing for a specific row and a specific column is the probability to go to Y while we're in X:

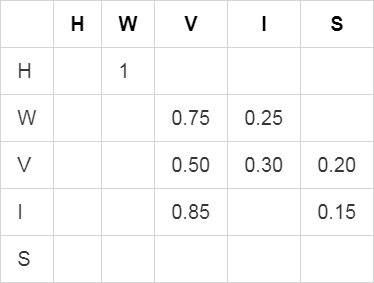
(I kept the 0 values blank so that it wouldn't be too hard to read)

The first row represent the probability to do the Y activity after coming home (H). Since I said that I always wash my hands (W) when I come home (H), the only probability that is higher than 0 is the washing hands (W) one. When I'm playing videogames (V), I either keep doing it for another hour, switch to playing an instrument (I) or go to sleep (S), which correspond to the third row.

We now have our probabilities. Indeed, in this table, since we represented the probability of switching activities every hour, it would mean that I wait one hour at home before washing my hands, then I wait one more hour before deciding to do something. This is unrealistic, but the example still stands nonetheless.

So, we have our events, we have our probabilities... Do we have a Markov Chain? Well, yes! Here is this a visualisation of this example:

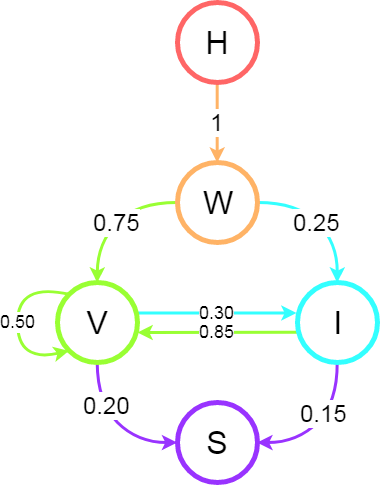
How does the concept of Markov Chain translates to sentences generation?

That's nice and all, but we still haven't talked about sentences generations. Now that you know what Markov Chains are, the rest is kinda easy to understand. As I said earlier, my bot first gather tweets from a person. I'm using tweets, but it could be any kind of input (for example, all the sentences from a book, a conversation between two people, etc.), as long as it's sentences.

We will use another example to explain how it works. Let say that we gathered these tweets:

• I am stupid
• I shat myself
• You are stupid and I don't like you
• You shat like I told you

These sentences are stupid, but it's not important. If we want that our generated sentences kinda look that these ones, we have to find a way to reproduce the way they are written. Problem is, we don't want to implement grammatical rules, basic syntax, etc. into our system: this would be very complicated and long. We want to keep it simple. A simple way to emulate the way these sentences are constructed is to, well... Use Markov Chains. Our events are the sentences words, and our probabilities to go from an event (a word) X to another event (another word) Y are the occurence of such transition in the sentences above. For example, the word " am " is only followed by the word " stupid ", so the probability to go from " am " to " stupid " is 1. The " I " can be followed by " am " (1 time), " shat " (1 time), " don't " (1 time) and " told " (1 time), so the probability to from " I " to each of these words will be 0.25 for each. Here is the corresponding table:

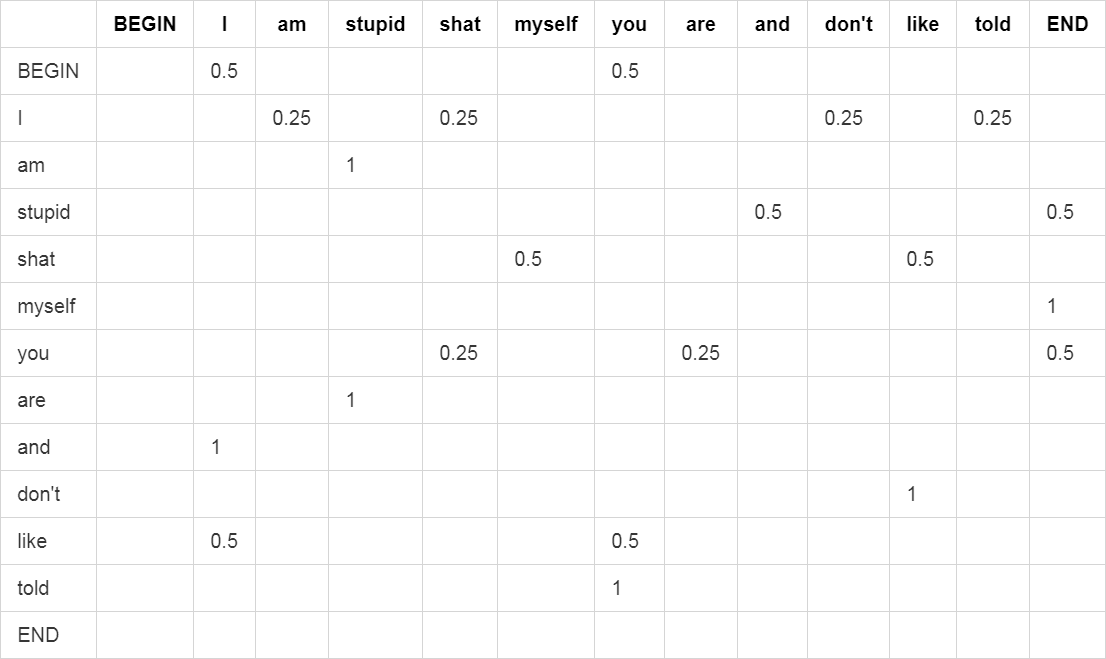
As you can see, we added " BEGIN " and " END " as " words ". These just mark the beginning and the end of the sentences. It helps keeping track of which words can be at the beginning of a sentence, and which words can end a sentence. Here, the sentence can start with either " I " or " You ", and can end with " stupid ", " myself " and " you ".

From here, we have everything we need to code our sentence generator! You can represent the data as the array above, or as objects (each objects is one word, and a list of possible next words with their probability, for example) if you prefer. The algorithm isn't hard to find:

1. Gather sentences from any source you want
2. Compute the probability matrix (as shown above)
3. Choose a word to begin the sentence (takr all words that follow the BEGIN keyword)
4. Randomly choose the next word from the list of the current word's probabilities
5. Stop when the END keyword is chosen

That's it. The algorithm is very simple. From the four sentences above, these are some that could be generated:

• I am stupid and I don't like you
• You shat like you are stupid
• I am stupid and I don't like you are stupid
• I shat myself
• I am stupid and I am stupid and I am stupid and I am stupid and I am stupid and I am stupid and I am stupid and I am stupid...

As you can see, the sentences aren't always coherent. Worse, you can be stuck in an infinite loop, like in the last example (it's like when you use the suggested words when typing on a smartphone's keyboard, you can eventually be stuck in an infinite loop repeating the same few words again and again). You should include another stop condition in the fifth step of the algorithm, to avoid these cases (although you should end up getting out of the loop). You can also have output sentences that are strictly indentic to the input ones. This one is pretty simple to eliminate: just get rid off the output sentences that are equals to the input ones.

Are we done yet?

Yes and No.

See, this example works, but it's hard to generate something coherent. One of the problems is that we only used 4 sentences to construct our probability matrix. In real cases, you want a lot of input sentences (so that you can generate a lot of different sentences). Another problem is about the algorithm: it only looks for the next word every time, to compute the probability matrix. In some sentences, it is acceptable to have the word Y after the word X, while it is not in other sentences. In every langages (that I know), rules have to be followed to make coherent sentences. We aren't looking into adding these rules into the algorithm to improve it. A simpler way to have better sentences is to compute the probability for n word to follow the word X. The bigger the n value, the more coherent the sentences will be, but there will be less variation in the output sentences (comparing to the original ones). In our case, we used n = 1. If we used n = 2, our matrix would look like this:

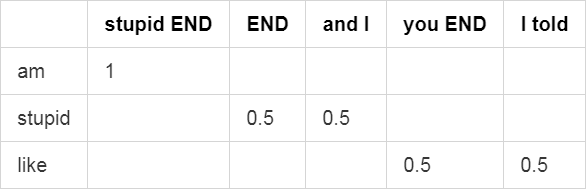
(I did NOT put the whole matrix, too big and messy)

While this limits the range of possible sentences, it generates much " realistic " ones. But be careful about the value of n: the higher it goes, the more input sentences you need.

I hope this small explaination about Markov Chains and how to generate sentences with them was clear and useful to you. Cheers!